Diagrams | Axel Gagge

Diagrams are sketches, sets of lines which are necessary to delineate the assemblages and set them into motion. They are close relatives – maybe even ancestors – of the letter, the image as well as the weave. Donna Haraway called them string figures: constructing them is a textile art, a thinking-practice where hand and mind follow each other.

Diagrams nakedly acknowledge that they are simplifications, patches pulled out from the big weave. They are like interfaces, lenses or rasters and work with connection rather than identification. They are machinic, not mechanical.

Diagrams depict and represent processes. A simple diagram of cause and effect: a sprinkler is turned on (A), causing the grass to become wet (B). A linear development of time. But we are not passive observers in the world, we are part of it. In order to make our choices, we have to consider counterfactuals: what could have happened and what is possible: what if A→C? Each choice is a fork, a branching of time. It forms a diagram, the tree.

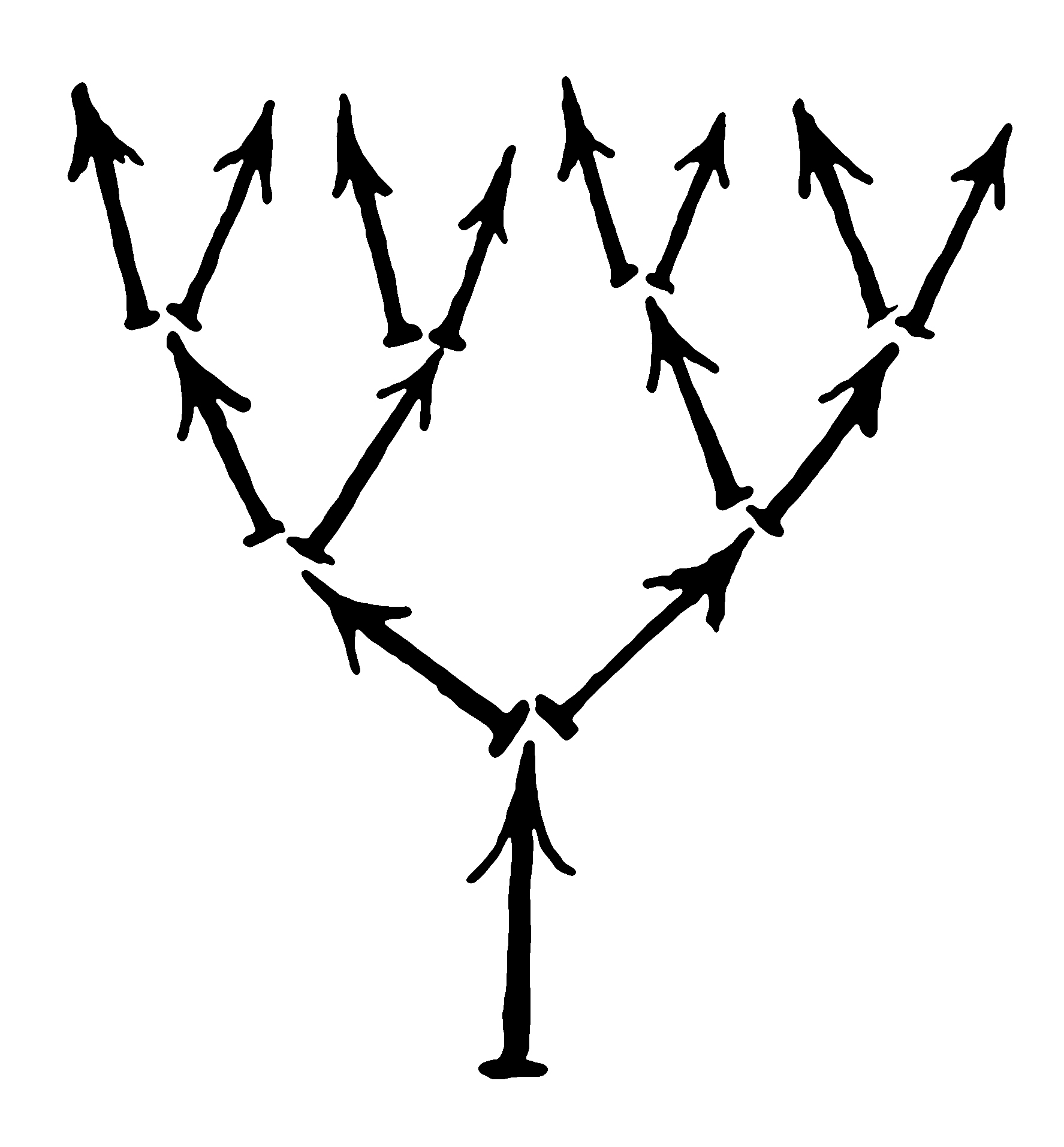
In many essays, Borges has written about books which include their own negation or even infinite books that include all possible variations on themselves. This is the nature of writing in general: we write in relation to our own counterfactual writing.

Up until recently, artificial intelligence (AI), statistics and even logic itself have all failed to grasp counterfactuals or causality. AI is instead built on the rudimentary idea of correlation, e.g., observing that grass becomes wet at the same occasions as the sprinkler was turned on. To try to teach machines about cause and effect, AI researchers have created special diagrams called Bayesian networks.

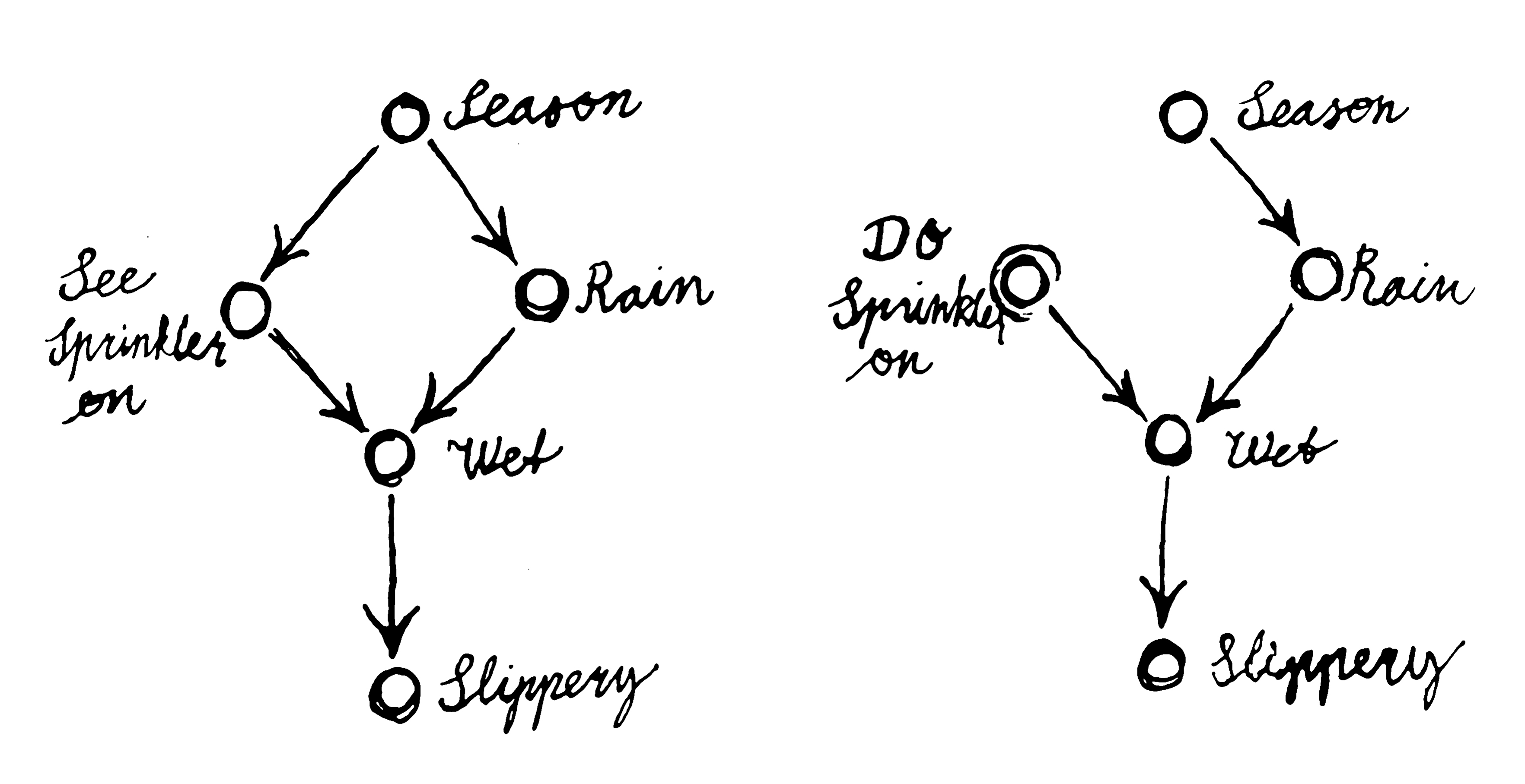
Variables (sprinklers, rain, etc.) are drawn as circles and connected by arrows which represent the possible relations of causality (the diagram above does not display all possibilities). To the left: the season may influence the rain or whether the sprinkler is on. This in turn can cause the grass to be wet and hence slippery. To the right: we contemplate the effect of turning a sprinkler on. This action is represented by cutting all incoming arrows to the sprinkler variable.

This practice of cutting in the diagram is especially important since it is where our agency comes in. Cutting different arrows corresponds to different possible actions. The technique allows us to understand cause and effect even in very complex situations. Using such diagrams, AI could soon be able to ask questions such as what if? and even why? But there are questions which machines could never answer.

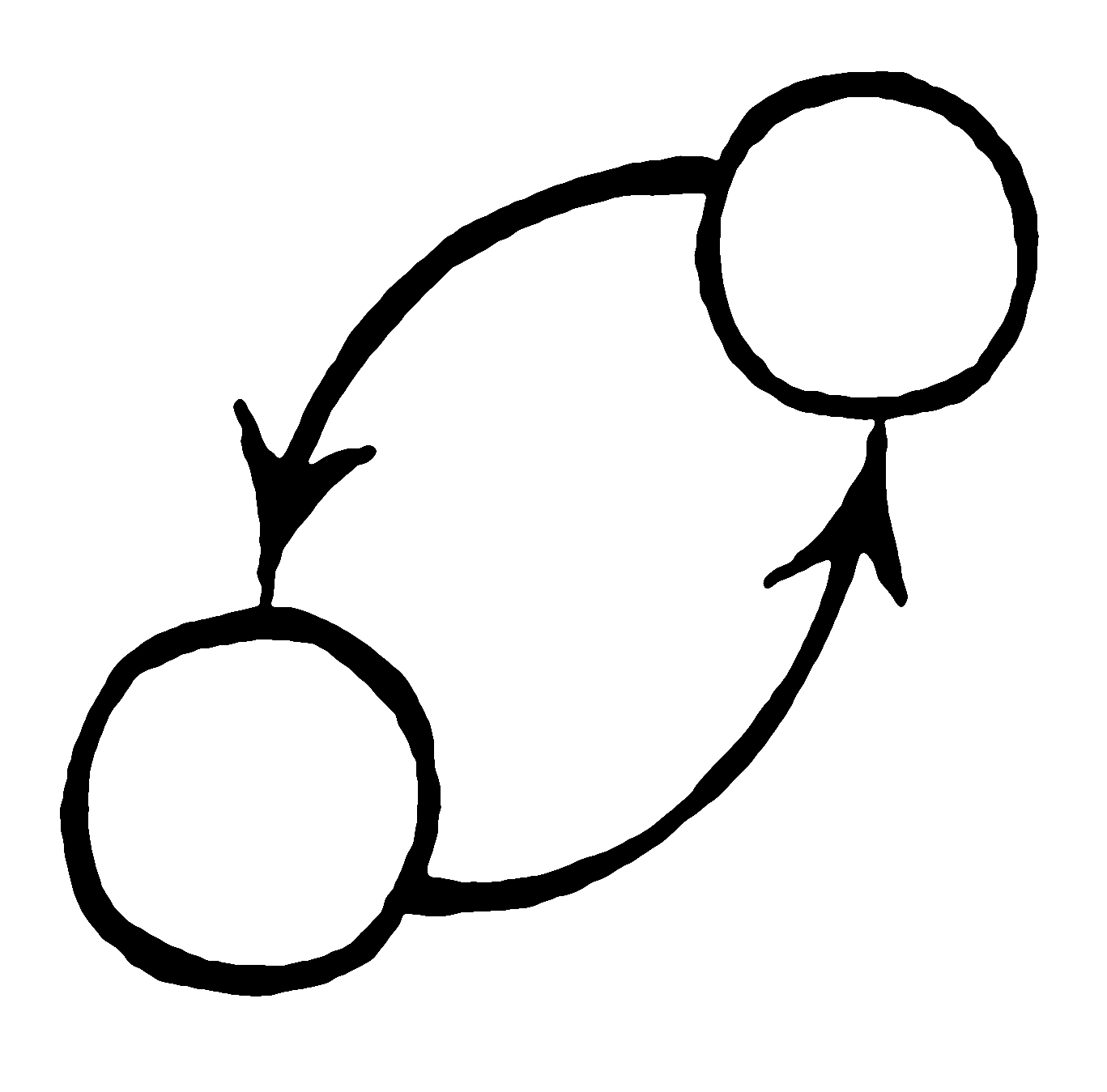
Computers can only grasp Bayesian networks if we don’t make any loops in them. The assumption is: if A causes B, it should be impossible that B causes A. In many cases, this is valid. Inside a mechanical clock, causality flows from the parts to the whole: it is the relation between pairs of cogs that combine to cause the hands of the clock to show the time.

But there are many situations in which causality forms loops, by flowing from the parts, to the whole and back again into the parts. In the living organism, causality flows back from the body to the cell, which listens to its environment and is capable of even reproducing the entire organism. The theoretical biologist Rosen mathematically proved that this makes living organisms fundamentally different from machines. He went on to show that the ability of self-reflection itself depends on such strange loops, also known under the name recursion.

Quantum physics is full of such strange loops. The result of a measurement depends on how the measurement was made: from the entire situation of the laboratory, causality flows into the measurement result. It is impossible to disentangle observer and quantum system. We are ourselves part of the Bayesian network.

Perhaps it is useful to keep in mind the Buddhist concept of interpenetration: everything develops together, in sym-poiesis. Indra’s net is an infinite weave with a pearl at the intersection between every pair of threads. Each pearl contains the infinite reflections of the infinitude of other pearls. If the world is a diagram, it is decorated with strange loops.